The report shows a previous checkpoint in the project’s life and will be updated soon to reflect the recent advancments. The formal report can be accessed here: pdf.

Motivation

Our project was motivated by the significant challenges in implementing machine learning on quantum systems using classical methods, which struggle with representing nonlinear activation functions. Tensor Networks offer a solution by using quantum circuits to efficiently implement ML tasks, allowing for ML to be conducted directly on quantum systems. This eliminates the need to transfer data from quantum sensors to classical computers, preserving the quantum information.

Furthermore, classical ML often encounters the "dimensionality curse," where the complexity increases exponentially with the number of dimensions. TNs, initially designed to represent high-dimensional quantum information, provide a way to mitigate this issue. They also naturally support parallel computation, which can further reduce the complexities of large tensor operations. Our project has leveraged these advantages to improve the performance and scalability of ML algorithms.

Milestones

For our first milestone we began by reviewing and identifying relevant literature for both TNs and ML to educate ourselves about how to achieve the project’s goal. We began with two sources in mind, Introduction to TN ¹, TN for ML (Google) ², and Supervised Learning with quantum inspired NNs. ³ For the next milestone, we moved on to apply this knowledge by using Qiskit to demonstrate how TNs perform in an image classification task. ⁴ We did this by using the implementation of the MPS topology for TNs based on the code in the Medium article. Next, we used RealAmplitudes from qiskit.circuit.library to create each block of the MPS which can be seen in Figure 1.

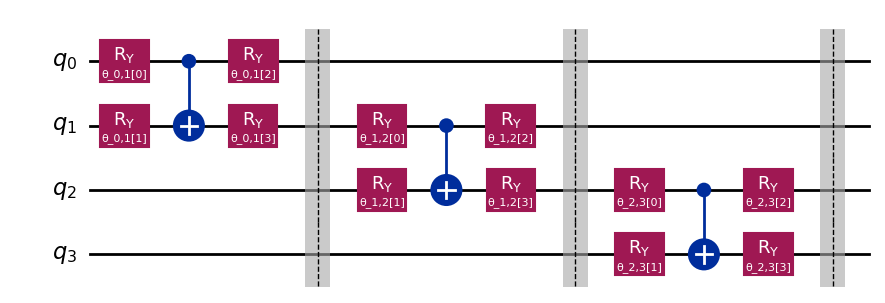
We then pre-reprocessed the input data using PCA before running the Qiskit code on an ideal simulation and on the simulated version of ibm_rensselaer backend implementing a variational classifier.

For our last milestone we implemented TNs in classical ML for image classification tasks utilizing the simple code examples provided by Google in their Github repository. In addition to the brief TensorNetwork documentation found in reference [9]. We started this process by getting familiar with TensorNetwork and the TensorFlow environment to understand the best practices we should utilize for the GPU option. Preprocessing the MNIST dataset was a step we made in order to enhance the performance of the model. Next, we encoded the image by flattening, normalizing and mapping the pixel values into 2 dimensional vectors. After encoding the image, we began to intialize the parameterized MPS network, with ReLu activation function at each node. Our last step in this process was to use the cross-entropy loss function, adam optimizer, and backpropagation methods provided by TensorFlow to train the model. We’ve also experimented by varying the compromised in bond dimension.

Results

In the quantum section of the project we all gained an understanding of TNs in relation to ML algorithms, specifically how they manipulate and represent quantum information.

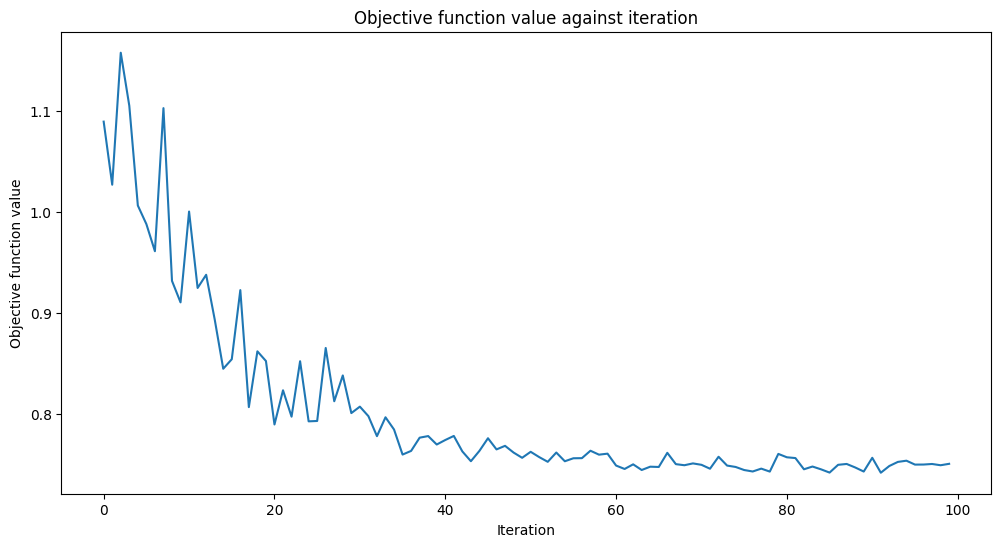
As a result of our work we have discovered the accuracy of the quantum algorithm with noise in our implementation. We have trained the QNN with MPS with 50 images per digit and had testing data of 1000 images per digit. Our experiments have measured and compared the accuracy in classifying digits three and six in a quantum neural network using matrix product state tensor networks. The results of these experiments are as follows: 80% accuracy for training data and 74.7191% of accuracy for testing data. The graph of our objective function over value can be seen below in Figure 2 and represents our qnn accuracy in guessing the correct digit either three or six based off the amount of iterations it goes through and trains on the set of 50 images per digit.

We have also implemnted the circuit on the ibm_rensselaer real backend but we believe that due to poor optimization of the circuits the following results, shown in Figure 3, were preliminarily achieved:

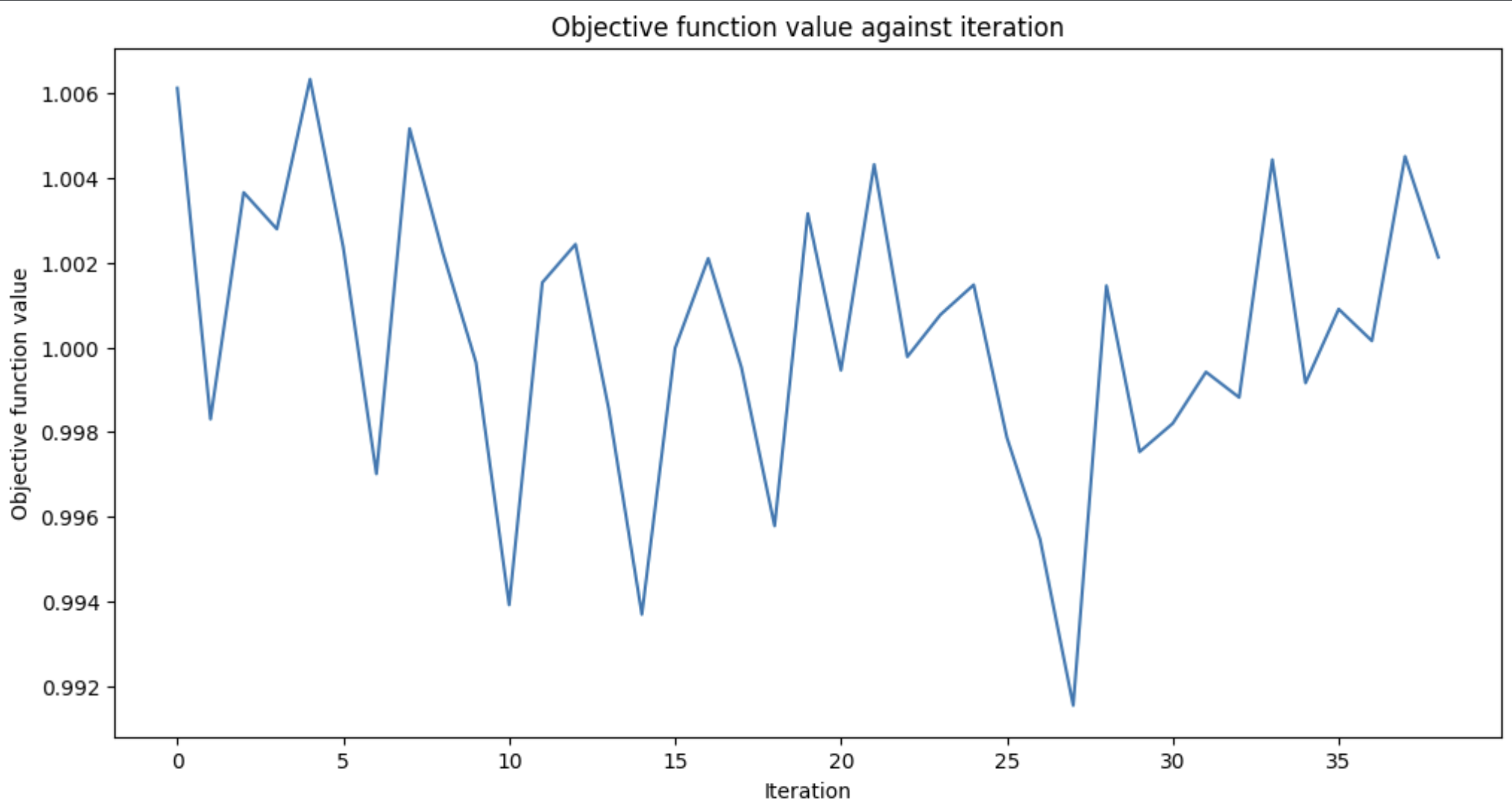
Figure 4 shows a snapshot of our recent quantum jobs submitted to the IBM Quantum Platform, executed on the ibm_rensselaer backend.

During our final presentation, our team has presented all relevant research about the inclusion of TNs inside ML tasks using techniques such as Matrix Products States (MPS) to efficiently represent the high-dimensional complex quantum states as well as our findings from experiments as mentioned previously. Additionally, we plan to compare computational speed to complete the task from the use of TNs in algorithms to classical algorithms for MNIST dataset that will be discussed more in the future direction.

In conclusion, our research has shown that TNs are highly effective for ML tasks, specifically on QC tasks of image classification tasks. While we have seen tremendous success with implementing tensor networks on quantum computer tasks, we have room for improvement on classical tasks. Once we have we have successfully implemented the model, we believe some potential applications which may benefit from this method include: Big data analytics, image and processing, and various other Optimization problems. There are many fields of application that rely on large amounts data that could benefit greatly from the improved computational speed and accuracy results that the inclusion of TNs in ML.

Future Direction

In regards to our work with Qiskit, we hope to optimize the quantum circuit on the ibm_rensselaer framework in the future. For reasons yet unknown, the Qiskit code as run on actual hardware does not see the same levels of performance that the simulator does; as such, moving forward, it is important to figure out why the quantum computer lacks the results that were initially simulated, and if such results are possible at all. Due to concern of under fitting the data set demonstrated by the low results, it may be worth modifying the sizes of the training and test image set.

In our work with the TensorNetwork library, we would like to improve upon the model we had developed in accordance with the research done by Google in the hopes of verifying the results claimed and explaining the reason for these results. We hope that the more accurate model will allow us to properly compare use of the TensorNetwork library against other forms of machine learning.

As it currently stands, however, much of the TensorNetwork library has gone undocumented, with many important sections of the library offering no clarification on how they work. Through our efforts in the classical space, we also hope to provide a well documented, open source example of the ideas in the TensorNetwork library article so that further research into the use of TNs in classical ML may have a better foundation.

Related Works

Tensor networks have seen successful implementation in physics and mathematics due to their efficient representation of high dimensional data [2]. Recently, it has also gained attention in applications like machine learning [1] which we aim to study and present in this project. To facilitate the application of TNs in ML, the TensorNetwork library was developed [1]. We have looked at many sources to understand TNs in both quantum and classical ML in addition to other tasks. In a quantum setting, the approach is to first encode the MPS network into a parameterized quantum circuit which is then trained using a quantum neural network [6]. The goal is to choose the phases of the rotational gates that will best replicate the TN. The circuit is then optimized to run on noisy intermediate-scale quantum hardware [5]. As for classical uses of TNs specific to classifying the MNIST dataset, we start by mapping the input into two dimensional vectors and contracting them with a parameterized MPS. The goal is to have the contraction, which will result in a 10 dimensional vector representing the ten classes, best predict the underlying classification task. The MPS is trained such that it will ultimately represent approximate a perfect classifier for the task [8]. By taking an inner product of the variational MPS and the encoded input data, the labels can be retrieved which we will then use to optimize the cross entropy objective function [1].

[1] Efthymiou, S., Hidary, J., & Leichenauer, S. (2019, June 7). [1906.06329] TensorNetwork for Machine Learning. Retrieved July 13, 2024, from arXiv.org website: https://arxiv.org/abs/1906.06329

[2] Stoudenmire, E. M., & Schwab, D. (2017, May 18). [1605.05775] Supervised Learning with Quantum-Inspired Tensor Networks. Retrieved July 13, 2024, from arXiv.org website: https://arxiv.org/abs/1605.05775

[3] Orús, R. (2014, June 11). [1306.2164] A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States. Retrieved July 13, 2024, from arXiv.org website: https://arxiv.org/abs/1306.2164

[4] [1812.04011] Tensor networks for complex quantum systems. (2019 22). Retrieved July 13, 2024, from arXiv.org website: https://arxiv.org/abs/1812.04011

[5] Dahale, G. R. (2023, May 24). Exploring Tensor Network Circuits with Qiskit | by Gopal Ramesh Dahale | Qiskit | Medium. Retrieved July 13, 2024, from Medium website: https://medium.com/Qiskit/exploring-tensor-network-circuits-with-Qiskit-235a057c1287

[6] Melnikov, A. A., Termanova, A. A., Dolgov, S. V., Neukart, F., & Perelshtein, M. R. (2023, June 19). Quantum state preparation using tensor networks. Retrieved August 7, 2024, from Quantum Science and Technology website: https://doi.org/10.1088/2058-9565/acd9e7

[7] Stoudenmire, M. (2022, Nov 2). Tutorial on Tensor Networks and Quantum Computing [Video]. YouTube. https://www.youtube.com/watch?v=fq3_7vBcj3g

[8] Stanford Quantum (2020, May 7). Tensor Network Workshop with Google X [Video]. Youtube. https://www.youtube.com/watch?v=NrvhGCkQnEs&list=LL&index=1

[9] TensorNetwork. (2019). TensorNetwork documentation. TensorNetwork. Retrieved August 18, 2024, from https://tensornetwork.readthedocs.io/en/latest/index.html